浅析分块 QR 分解的原理与一般高性能实现

引用

本文在书写时主要参考了

https://ieeexplore.ieee.org/document/6877344

首先我们先搞定什么是 QR 分解

QR 分解的定义

设 $A \in \mathbb{C}_n^{m\times n}$，则 $A$ 可唯一地分解为 $A = QR$ 其中，$R$ 是 $n$ 阶正则上三角矩阵，$Q \in Q_n^{m\times n}$。

我们只要能找到这么一种构造就可以找到 QR 分解，其实 Householder 向量就为我们提供了这么一种构造，那么什么是 Householder 向量呢？为什么说他可以为我们提供一种构造呢？

对于一个向量 $v$，我们构造出一个反射矩阵 $H$：

$H = I - 2\frac{vv^{\mathsf{T}}}{v^{\mathsf{T}}v}$

这个矩阵 $H$ 是正交矩阵（$H^{\mathsf{T}} H = I$）。

其中 $v$ 是 Householder 向量，决定了反射的方向。通过这个反射矩阵，任何向量 $x$ 都会被映射到一个新的向量 $x'$，而我们希望这个新的向量 $x'$ 在 $e_1$ 方向上有非零分量，其他方向上的分量为零。

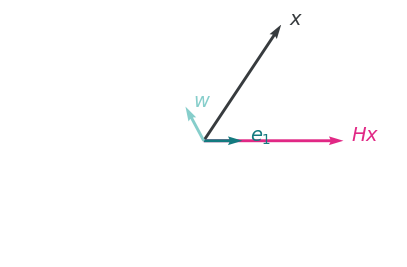我们简单地观察就可以发现，只需要构造 $w = |x| e1 - x$ 就可以找到这个完美的反射用的 $w$，随后就可以做到 $Hx = |x| e1$ 。我们构造出这个 $H = I - 2\frac{vv^{\mathsf{T}}}{v^{\mathsf{T}}v}$ 后就可以用它来针对性地获得我们想要的分量了。同时 $H$ 还是个酉矩阵，所以最后就能转换成矩阵连乘，这也给出了一种计算 QR 分解的算法。

相当于在这里逐行做我们的 Householder 变换，然后下三角存储我们的 Householder 向量（其实相当于把消元得到的 R 矩阵的下三角利用起来，存每次的 Householder 变换），上三角则存储我们 QR 分解的 R。

那我们就知道了，只要这样做 Householder 变换我们可以拿到我们的 Householder 向量构造成的 Q。

但是对于 GPU 来说，我们必须去解除依赖，那么最好一块只对一个矩阵进行运算。所以我们可以写一个 block 级别的 Householder 的 QR 分解作为我们的最小单元。

剩下的算法口述比较复杂，见下面的推导

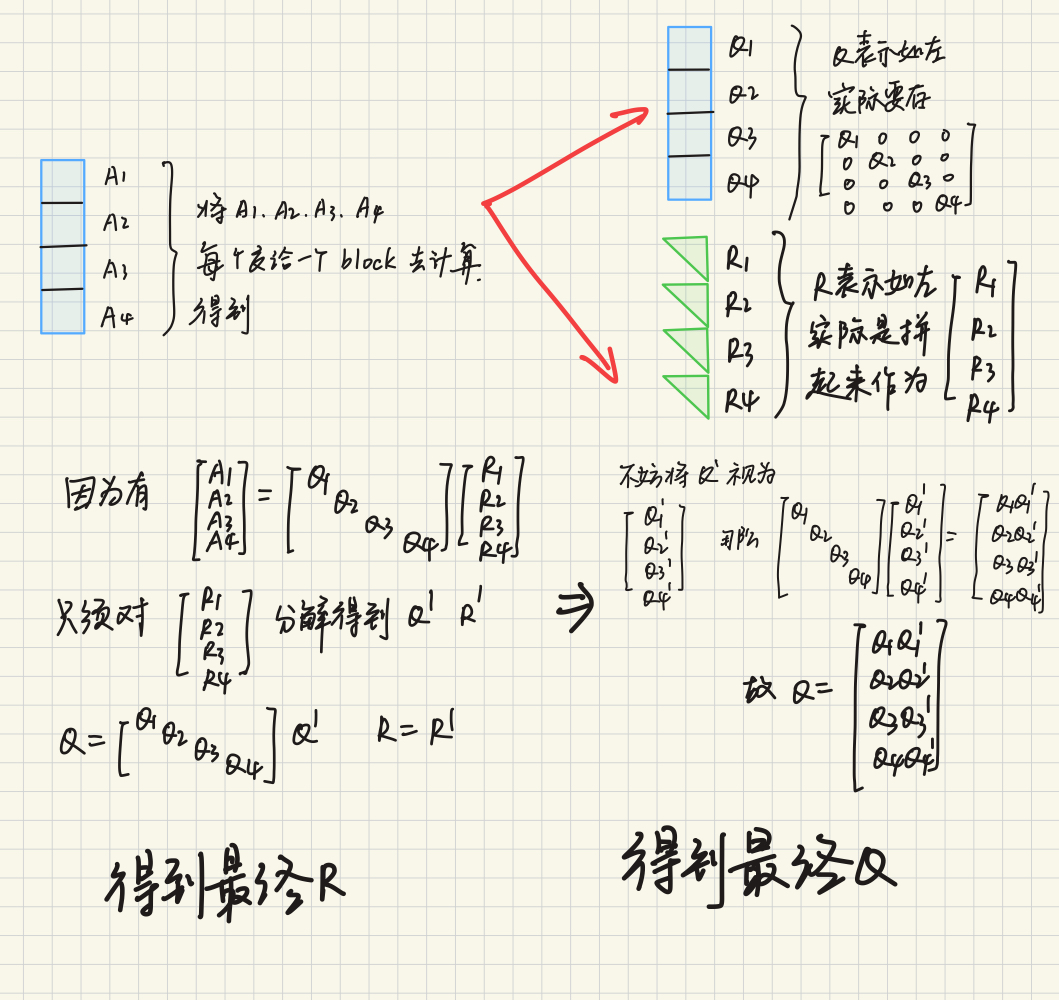
使用上面的技术，我们就可以实现一个高性能的 tsqr。

这时候，我们就可以去处理任意高的 QR 分解了，接下来我们要基于上面的 tsqr 处理任意宽的 QR 的分解。