CUDA Programing Guide 阅读笔记

因为在 CUDA 13 后似乎我们的 CUDA Programing Guide 做了一次更新，而且离上次看 CUDA Programing Guide 过了很久了，常说书读百遍，其义自现。所以这里打算再读一遍。

本身就已经分成了五个 Parts，分别是 Introduction and Programing Model Abstract，Programing GPUs in CUDA，Advanced CUDA，CUDA Features 和 Technical Appendices。

我们先做一个概览，Introduction and Programing Model Abstract 可以带你快速阅读一下 CUDA 的编程模型，然后是教你如何入门写一个简单的 SIMT Core，往后是重要的 CUDA APIs 以及 Kernel Programing，接着 CUDA Features 则是给了你很多深度使用 CUDA 的能力，再往后则是一些技术性的附录。

Introduction and Programing Model Abstract

最初的 GPU 是为了图形处理，但是后来发现他也可以用来做通用计算。这要从他的特性聊起，他牺牲了单个线程的能力，来大幅度提高对应的并行度，从而在很多任务中，性能大幅超过 CPU。现在当然也有类似 Nvidia 自己的 Warp 和 OpenAI 的 Triton。

https://github.com/NVIDIA/accelerated-computing-hub?tab=readme-ov-file

那么我们怎么学习 CUDA 呢，这里有一个 nvidia 新给的仓库，里面可以支持你在 colab 直接用对应的 GPU 进行学习。

不过这里按下不表，下面会专门的篇幅介绍这个课程。

包括 Programing Model 之类的，我觉得通过 Fundamentals of Accelerated Computing with Modern CUDA C++ 可以获得更好的认识。

Fundamentals of Accelerated Computing with Modern CUDA C++

下面我们主要根据这个课来讲解下，现代 CUDA C++ 怎么完成对应的工作。

Execution Spaces

首先先教你如何实现一个 elementwise 开始。如果是 CPU 的代码，我们一般会这么写：

#include <cstdio>
#include <vector>

int main() {
    float k = 0.5;
    float ambient_temp = 20;
    std::vector<float> temp{ 42, 24, 50 };

    std::printf("step  temp[0]  temp[1]  temp[2]\n");
    for (int step = 0; step < 3; step++) {
        for (int i = 0; i < temp.size(); i++) {
            float diff = ambient_temp - temp[i];
            temp[i] = temp[i] + k * diff;
        }

        std::printf("%d     %.2f    %.2f    %.2f\n", step, temp[0], temp[1], temp[2]);
    }
}

我们创建了一个 std::vector，然后对这些做了一个逐元素操作(elementwise)。

这个操作是什么呢？就是让这个元素更加接近 20，每次都减半对应的距离。

不同的 CPU 支持不同的指令集，在 x86 的 CPU 上 temp[i] + k * diff 会被编译成 vfmadd132ss 而在 arm CPU 上会被编译为 vmla.f32。当然，GPU 也有对应的指令集。

下面的图片介绍了这个在不同的设备上会怎么执行：

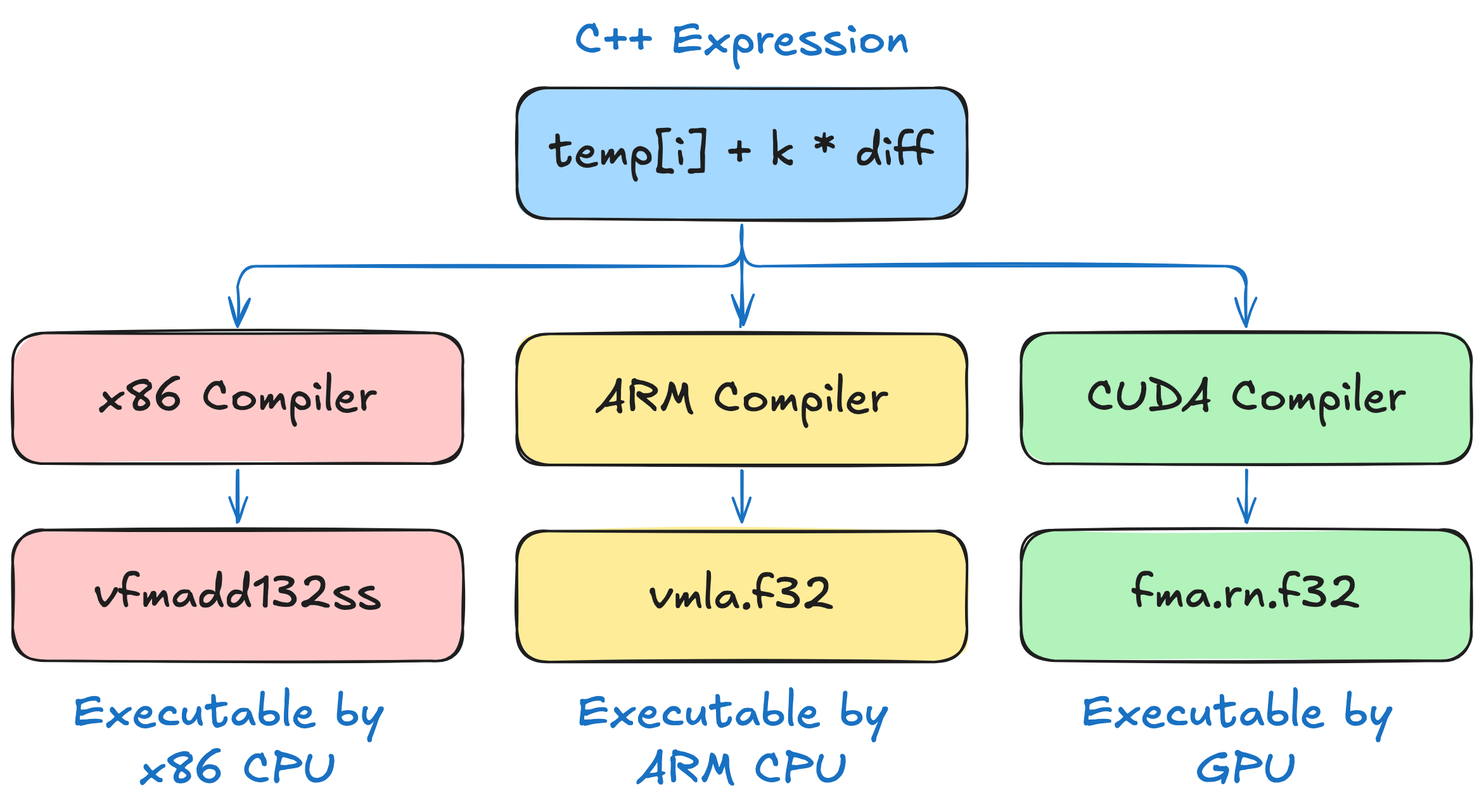
但是我们的 GPU 更接近于加速器而不是独立的处理器，所以我们要执行对应的任务的时候一般需要从 CPU 启动对应的任务，随后 launch 到 GPU 上，最后实际上在 GPU 上执行。

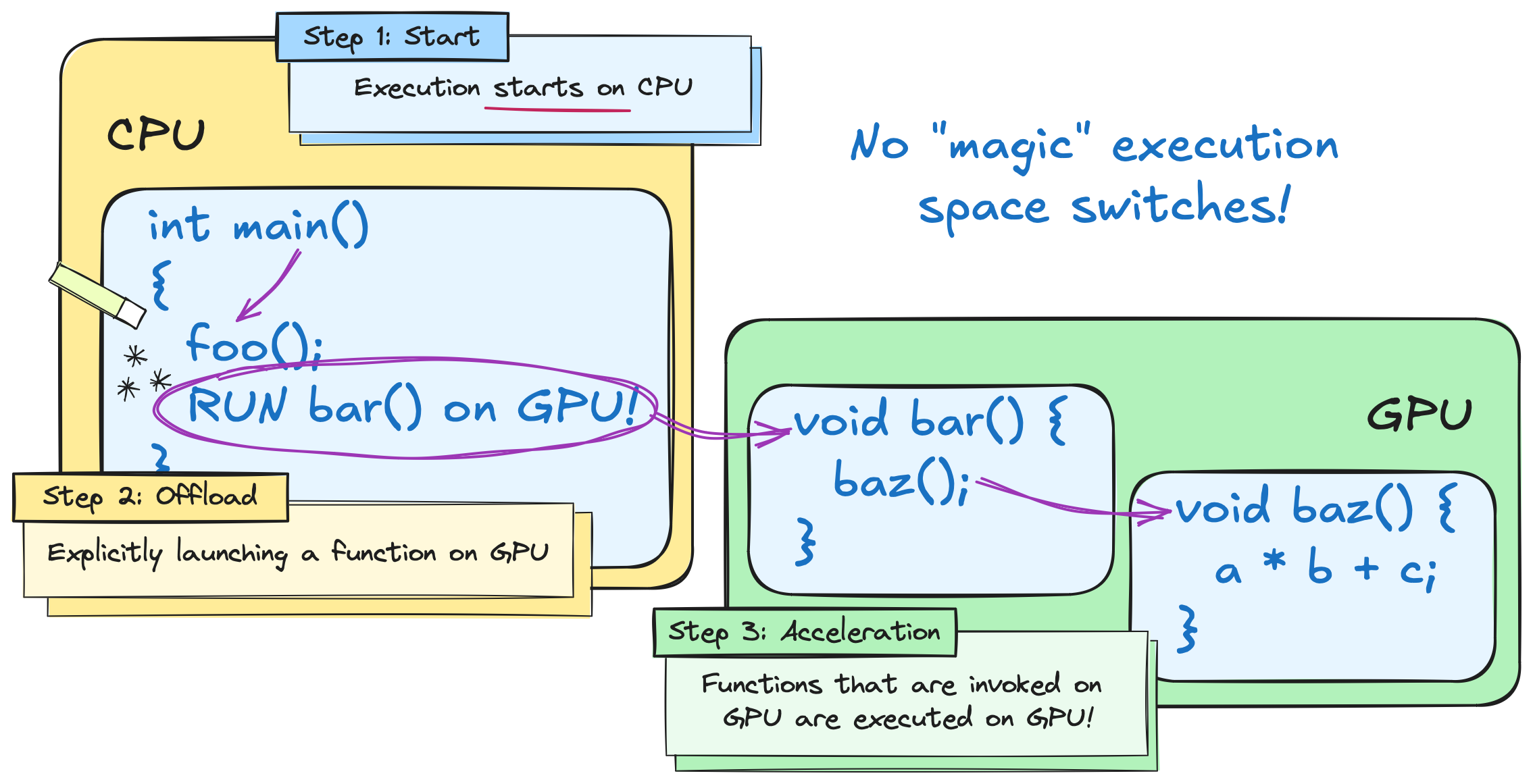
这就带来了不同的执行空间，我们在 CPU 侧称之为 host 在 GPU 侧称之为 device。

NVCC 对 C++ 进行了扩展，允许指出哪些代码是在 device 侧执行的。

对于上面的代码，我们可以用 stl 重写成利用 std::transform 的版本。

#include <algorithm>
#include <cstdio>
#include <vector>

int main() {
    float k = 0.5;
    float ambient_temp = 20;
    std::vector<float> temp{ 42, 24, 50 };
    auto transformation = [=] (float temp) { return temp + k * (ambient_temp - temp); };

    std::printf("step  temp[0]  temp[1]  temp[2]\n");
    for (int step = 0; step < 3; step++) {
        std::transform(temp.begin(), temp.end(), temp.begin(), transformation);
        std::printf("%d     %.2f    %.2f    %.2f\n", step, temp[0], temp[1], temp[2]);
    }
}

当我们用 CUDA 的办法去写，就可以直接换成下面的代码。

#include <thrust/execution_policy.h>
#include <thrust/universal_vector.h>
#include <thrust/transform.h>
#include <cstdio>

int main() {
    float k = 0.5;
    float ambient_temp = 20;
    thrust::universal_vector<float> temp{ 42, 24, 50 };
    auto transformation = [=] __host__ __device__ (float temp) { return temp + k * (ambient_temp - temp); };

    std::printf("step  temp[0]  temp[1]  temp[2]\n");
    for (int step = 0; step < 3; step++) {
        thrust::transform(thrust::device, temp.begin(), temp.end(), temp.begin(), transformation);
        std::printf("%d     %.2f    %.2f    %.2f\n", step, temp[0], temp[1], temp[2]);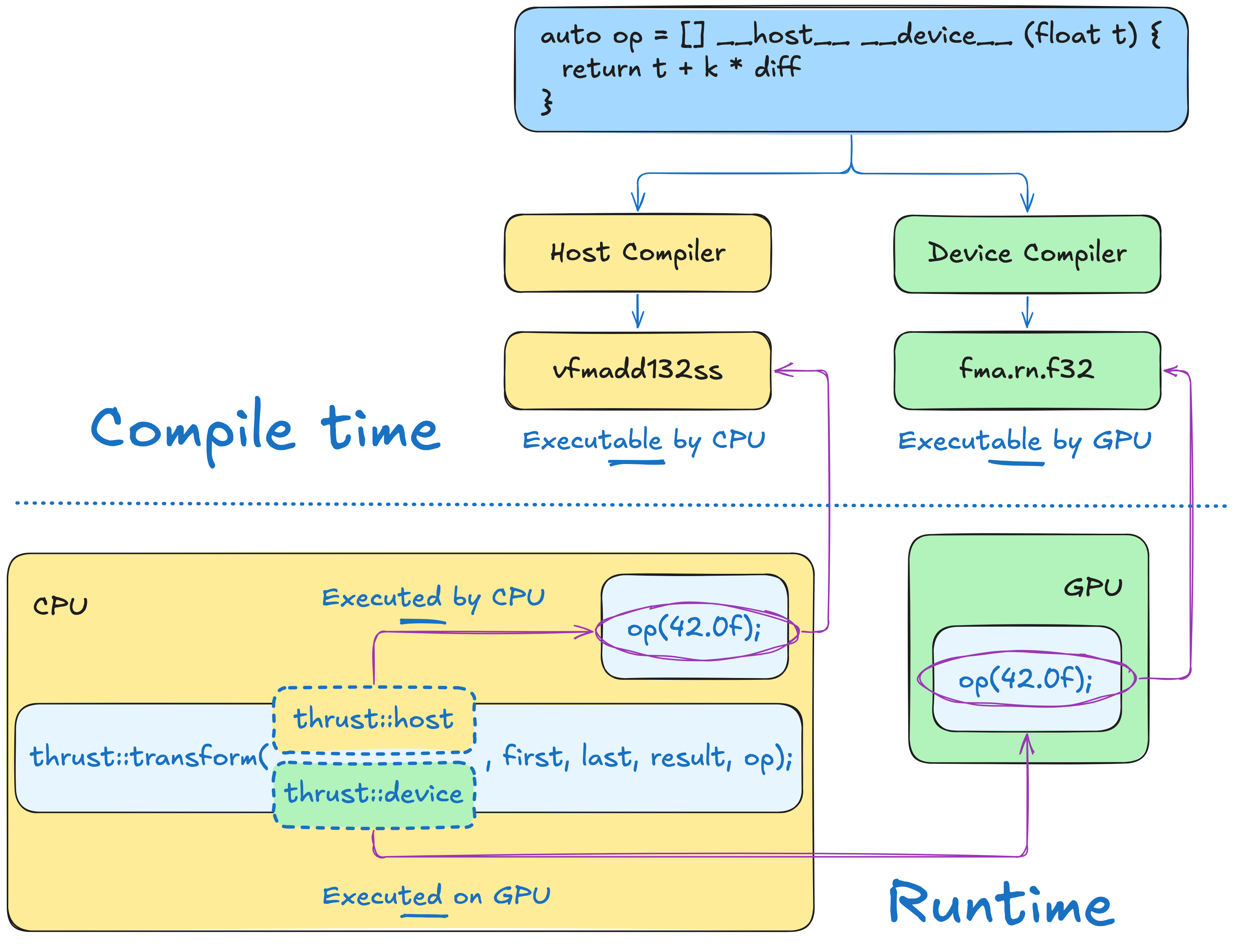
    }
}

也就是说，我们最后如何执行，都是看我们怎么指定，不过我们要预先告诉编译器是怎么干的。这个有对应的练习，可以在 nvidia 的仓库找到

Extending Algorithms and Lazy Evaluation

在前面的练习中，我们知道了怎么用 thrust 去替换掉一些 standard 的方法，在这节课，我们要用来处理一些复杂一些的方法，这就要用到 vector 的迭代器了。

这样子也可以通过传递一个 lambda 表达式来自定义 functor。

#include "ach.h"

float naive_max_change(const thrust::universal_vector<float>& a,
                       const thrust::universal_vector<float>& b)
{
    // allocate vector to store `a - b`
    thrust::universal_vector<float> unnecessarily_materialized_diff(a.size());

    // compute products
    thrust::transform(thrust::device,
                      a.begin(), a.end(),                       // first input sequence
                      b.begin(),                                // second input sequence
                      unnecessarily_materialized_diff.begin(),  // result
                      []__host__ __device__(float x, float y) { // transformation (abs diff)
                         return abs(x - y);
                      });

    // compute max difference
    return thrust::reduce(thrust::device,
                          unnecessarily_materialized_diff.begin(),
                          unnecessarily_materialized_diff.end(),
                          0.0f, thrust::maximum<float>{});
}

int main()
{
    float k = 0.5;
    float ambient_temp = 20;
    thrust::universal_vector<float> temp[] = {{ 42, 24, 50 }, { 0, 0, 0}};
    auto transformation = [=] __host__ __device__ (float temp) { return temp + k * (ambient_temp - temp); };

    std::printf("step  max-change\n");
    for (int step = 0; step < 3; step++) {
        thrust::universal_vector<float> &current = temp[step % 2];
        thrust::universal_vector<float> &next = temp[(step + 1) % 2];

        thrust::transform(thrust::device, current.begin(), current.end(), next.begin(), transformation);
        std::printf("%d     %.2f\n", step, naive_max_change(current, next));
    }
}

像这样一段代码，我们确实利用对应的函数完成了，但是写起来很麻烦，事实上我们可以用内置的方法进行简化。

包括：

counting_iterator: 返回对应的索引
transform_iterator: 实现对应的 operator 可以对原来数据的底层 array 进行操作
zip_iterator: 则可以把两个相关的数组绑在一个 tuple 里面
transform_output_iterator: 当然还可以对原数据进行修改
discard_iterator: 也可以对一些数据进行忽略

#include "ach.h"

float naive_max_change(const thrust::universal_vector<float>& a,
                       const thrust::universal_vector<float>& b)
{
    thrust::universal_vector<float> diff(a.size());
    thrust::transform(thrust::device, a.begin(), a.end(), b.begin(), diff.begin(),
                      []__host__ __device__(float x, float y) {
                         return abs(x - y);
                      });
    return thrust::reduce(thrust::device, diff.begin(), diff.end(), 0.0f, thrust::maximum<float>{});
}

float max_change(const thrust::universal_vector<float>& a,
                 const thrust::universal_vector<float>& b)
{
    auto zip = thrust::make_zip_iterator(a.begin(), b.begin());
    auto transform = thrust::make_transform_iterator(zip, []__host__ __device__(thrust::tuple<float, float> t) {
        return abs(thrust::get<0>(t) - thrust::get<1>(t));
    });
    return thrust::reduce(thrust::device, transform, transform + a.size(), 0.0f, thrust::maximum<float>{});
}

int main()
{
    // allocate vectors containing 2^28 elements
    thrust::universal_vector<float> a(1 << 28);
    thrust::universal_vector<float> b(1 << 28);

    thrust::sequence(a.begin(), a.end());
    thrust::sequence(b.rbegin(), b.rend());

    auto start_naive = std::chrono::high_resolution_clock::now();
    naive_max_change(a, b);
    auto end_naive = std::chrono::high_resolution_clock::now();
    const double naive_duration = std::chrono::duration_cast<std::chrono::milliseconds>(end_naive - start_naive).count();

    auto start = std::chrono::high_resolution_clock::now();
    max_change(a, b);
    auto end = std::chrono::high_resolution_clock::now();
    const double duration = std::chrono::duration_cast<std::chrono::milliseconds>(end - start).count();

    std::printf("iterators are %g times faster than naive approach\n", naive_duration / duration);
}

虽然只是简单的包装了一层，但是后面的远快于前面的，因为这里我们用迭代器包了一层，转换迭代器的优点是只有在解引用的时候才会计算，这就是 CUDA 的 Lazy Evaluation，减少了访存，但是增加了计算，在 GPU 上是很有性价比的。在现代 C++ 中，我们往往也用得到这些技巧，不过我们这里需要知道的是 CUDA 的这些基本都是 Lazy Evaluation。